Ｒｙｎのページ（商業高校情報教育研究室）

正規分布

ヨノナカの様々な事象において、 その母集団の或る数値的な項目が「平均が μ、分散が σ² である 正規分布（の各公式）に従う（当て嵌まる）と見做す」事で、 様々な統計分析を行う為の、確率分布の一つ。ガウス分布とも呼ばれる。 特に、平均 μ が０、分散 σ² が１である分布を、標準正規分布と言い、 統計処理で「確からしさ」「信頼性」「誤差」などを調べる際に、よく使われる。 標準正規分布の確率の値の表や、正規分布の値から標準正規分布の値へ変換する公式も有る。

中央極限定理

元の母集団の分布が実際はどのような分布（一様分布、二項分布、ポアソン分布、指数分布、其の他色々） に従っていたとしても、抽出するサンプルサイズｎの値が充分に大きければ、その標本平均の分布 （同じ母集団から全ての組み合わせでｎ個の抽出をして得られる標本の各々の平均の分布。 現実的には不可能な場合が殆どなので、充分な回数（サンプル数）で無作為に抽出する。）は、 近似的に、母集団の平均 μ と等しく、標本分散 σ² は 母集団の分散 σ² ｎ である正規分布（の公式）に従うと見做す事が出来る、 更に、もし母集団分布が正規分布であった場合は、ｎの大きさによらず、 近似的にでもなく、正規分布に従う、という理論（中心極限定理という）に基いている。

例えば、沢山のサイコロの中から無作為に１回を取り出し振る事を何度も繰り返す試行を行う場合、 理論の上の計算では、
１から６までの各々の目が出る確率は １ ６ で一様分布となり、その期待値（平均）は １＋２＋３＋４＋５＋６ ６ ＝ ７ ２ ＝ ３．５、
分散は、 (1- 7 2 )²+(2- 7 2 )²+(3- 7 2 )²+(4- 7 2 )²+(5- 7 2 )²+(6- 7 2 )² ６ ＝ ３５ １２ ＝２．９１６６６．．．であるが、
サイコロを無作為に２個取り出し振る事を何度も繰り返す場合、２個の出た目の平均となる確率は、１と６が各々 １ ３６ で最も低く、３．５が ６ ３６ ＝ １ ６ で、最も高くなる、山型の分布になる。 （ 分散は ３５ １２×２ ＝ ３５ ２４ ）
サイコロを振る回数ｎを増やすほど、分布の平均が３．５、分布の分散が ３５ １２ｎ の正規分布に近づく。

サイコロは、１回に出る目が６通りしかなく、その出方も一様な為に、 予め理論から上記の様な確率計算が出来るが、 ヨノナカの様々な事象は非常に複雑なので、 実際に何度も母集団から同様な標本の抽出を繰り返し、 正規分布に従うと見做す事で、様々な統計分析を行う事になる。

正規分布の特徴は、

• 平均値 μと最頻値と中央値が一致する。
• 平均値 μを中心にして左右で線対称である。
• x軸が漸近線（ｘ軸に接しない）である。
• 分散 σ²（標準偏差 σ）が大きくなると、曲線の山は低くなり、左右に広がって平らになる。 分散 σ²（標準偏差 σ）が小さくなると、山は高くなり、よりとんがった形になる。
• μ±1σ の範囲の中に全体の約68％、μ±2σ の範囲の中に全体の約95％、 μ±3σ の範囲の中に全体の約99.7％、が含まれており、信頼性や品質管理などに利用される。

などである。

pythonで、サイコロの例を乱数でシミュレーションしてグラフを描いてみる。
サンプルサイズｎと、繰り返す回数（サンプル数）を入力すると、 サイコロの目の平均の分布のグラフが描かれる。
敢えて、判り易くしてある。 あくまでも乱数によるシミュレーションなので、誤差は出る。

# dice.py  by Ryn    Nov. 9, 2022

import random
import math
import matplotlib.pyplot as plt

cnt = []
cntlabel = []
total = 0
variance = 0

print()
n = int(input('　サンプルサイズ（ｎ） --> '))
m = int(input('　サンプル数 --> '))

for i in range(6 * n - (n - 1)):
    cnt.append(0)
    cntlabel.append((i + n)/ n)

for i in range(m):
    dice = 0
    for j in range(n):
        dice += random.randint(0, 5)
    cnt[dice] += 1

for i in range(len(cnt)):
    print('　%1.2f : %6d' % (cntlabel[i], cnt[i]))
    total += cntlabel[i] * cnt[i]
average = total / m
print('　平均 : %1.5f' % ( average ))

for i in range(len(cnt)):
    variance += (( average - cntlabel[i] ) ** 2) * cnt[i] 
variance /= m
print('　分散 : %1.5f' % variance )
print('　標準偏差 : %1.5f' % math.sqrt(variance) )

for i in range(len(cnt)):
    cnt[i] /= m

fig = plt.figure(dpi=150)
plt.title('「サイコロを' + str(n) + '回振って出た目の平均」の分布（' + str(m) + "回繰り返す）", fontname="MS Gothic")
plt.xlabel("目の平均", fontname="MS Gothic")
plt.ylabel("確\n率", fontname="MS Gothic", rotation=360)
plt.bar(cntlabel, cnt, width=0.5/n, align='center')
plt.xlim(0.5, 6.5) 
plt.ylim(0, max(cnt) * 1.2) 
plt.show()

実行例。
　
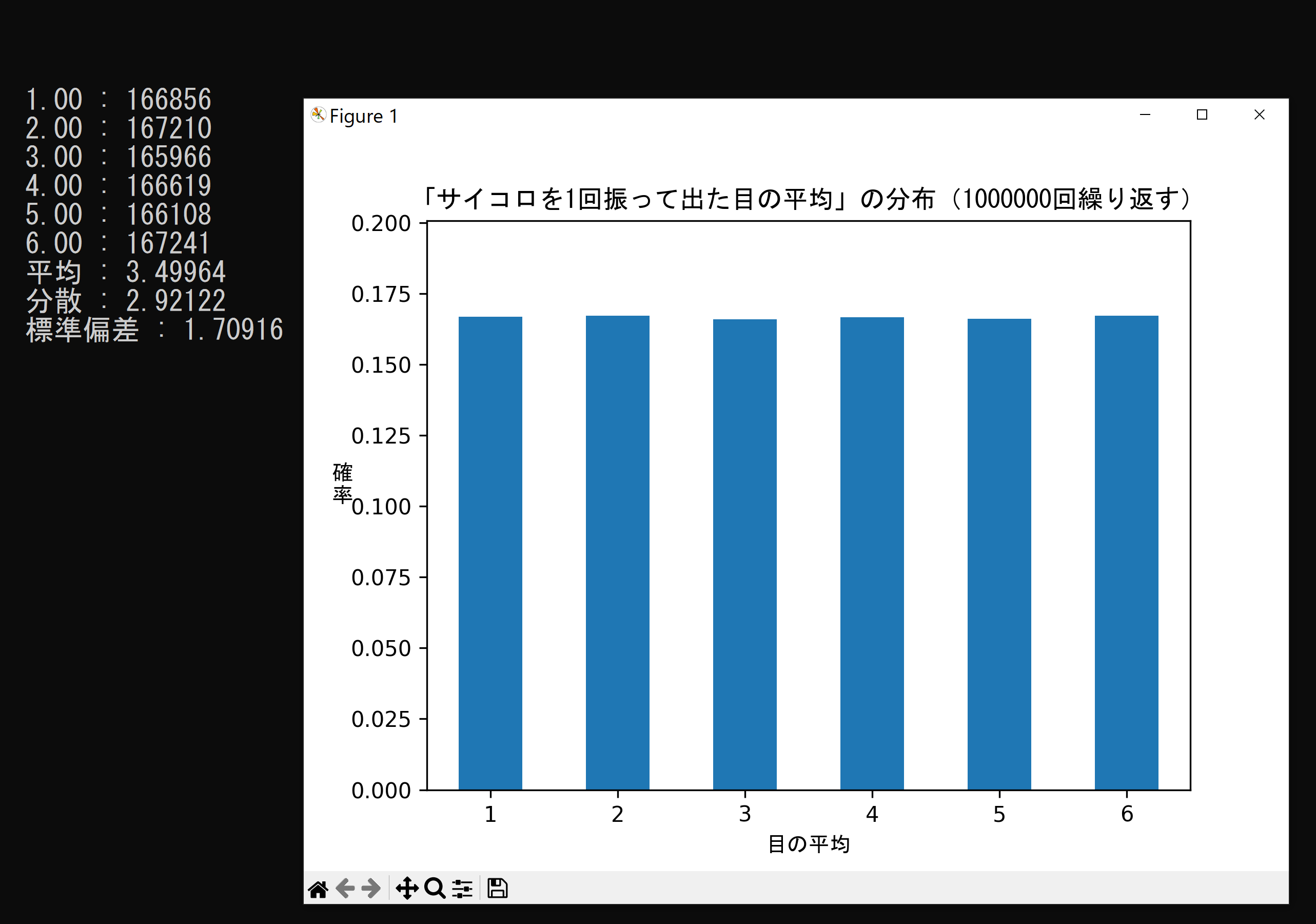
サンプルサイズｎ＝１、サンプル数＝ 1,000,000
多くのサイコロの中から無作為に１個を取り出し振る事を繰り返す時の目の平均（出た目そのもの）の分布は、 サイコロや振った人がイカサマで無ければ、一様分布に近似する。


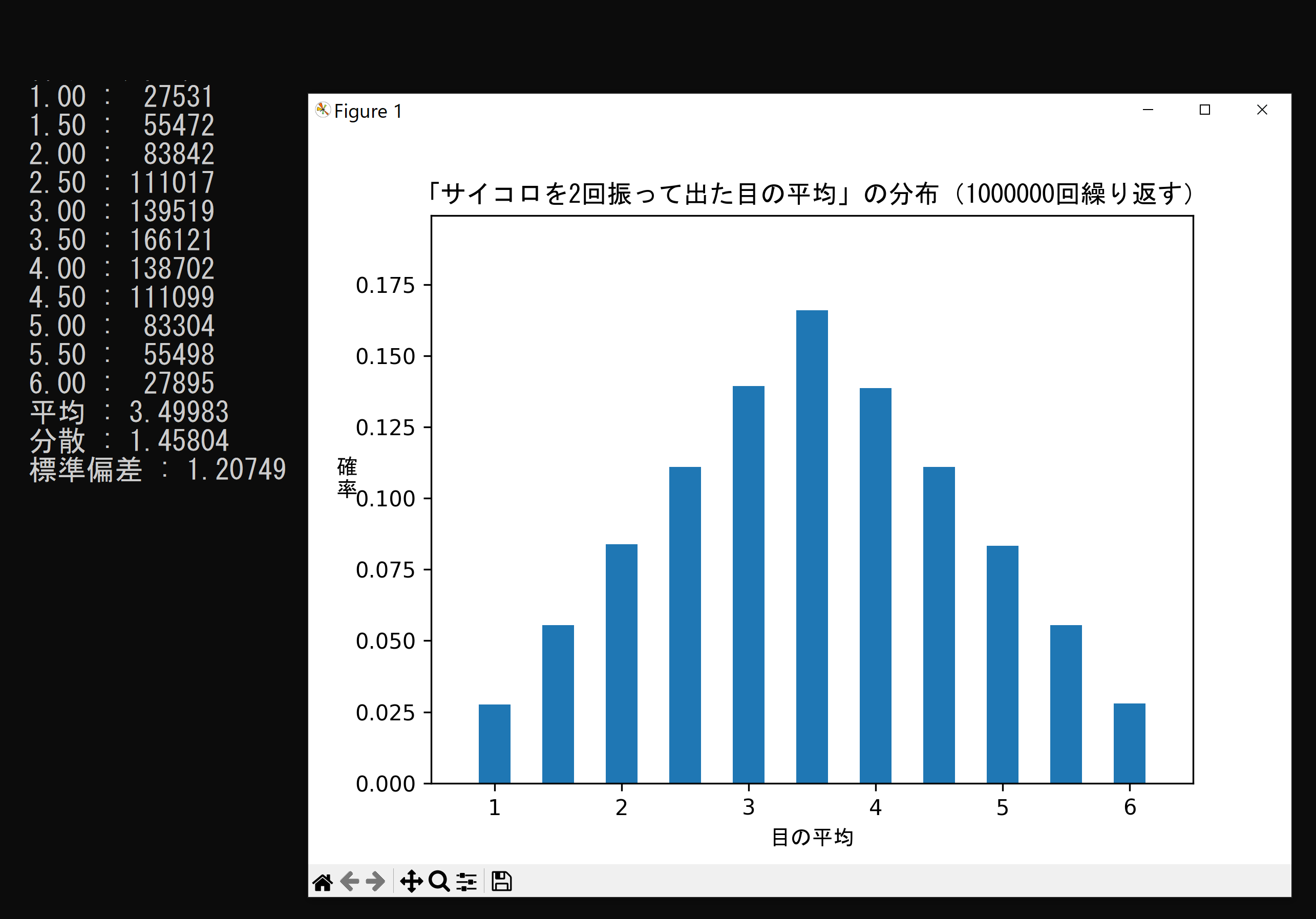
サンプルサイズｎ＝２、サンプル数＝ 1,000,000
多くのサイコロの中から無作為に２個取り出し振った目の平均の分布。
平均値 μと最頻値と中央値が（ほぼ）一致する。


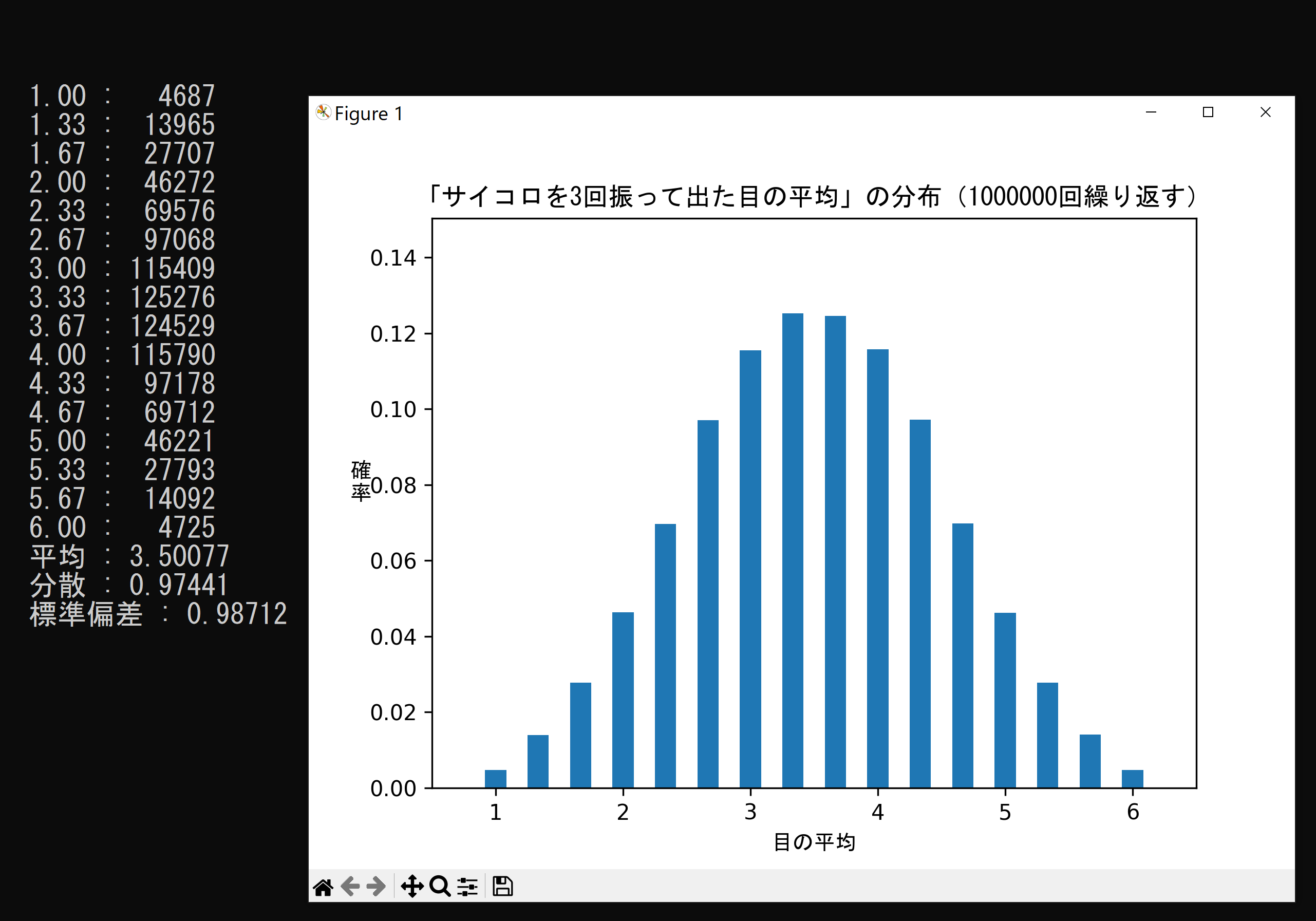
サンプルサイズｎ＝３、サンプル数＝ 1,000,000
多くのサイコロの中から無作為に３個取り出し振った目の平均には 3.5 という値は存在せず、 また、その平均は、割り切れないものが多く有る為、 このプログラムでは、分布の平均、分散、標準偏差で誤差が出る可能性が有るが、 とりあえず、分布の平均は、3.5に近似する。


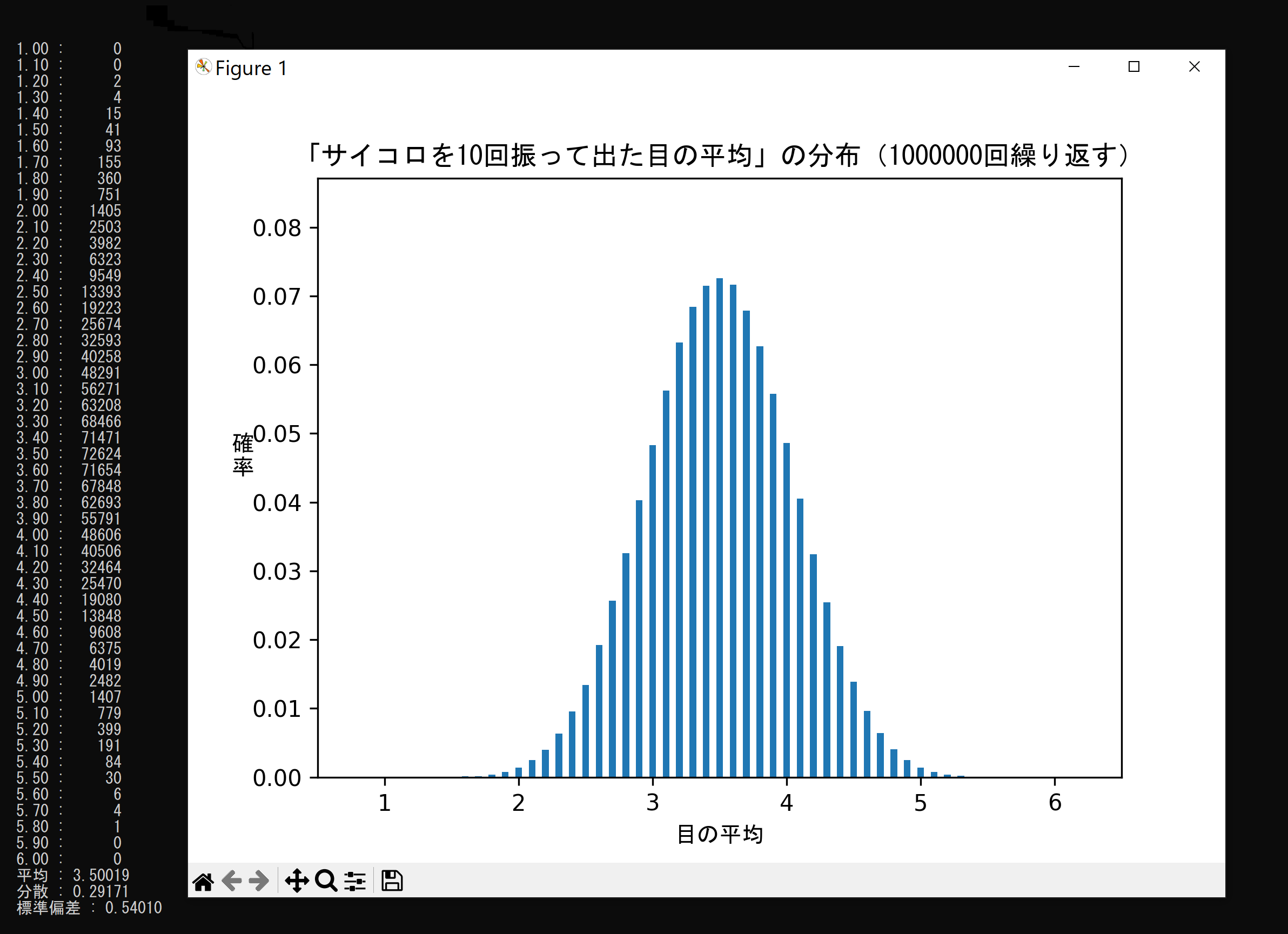
サンプルサイズｎ＝１０、サンプル数＝ 1,000,000
多くのサイコロの中から無作為に１０個取り出し振った目の平均の分布。 乱数によるシミュレーションなので０回が有るが、決して１回未満で有ってもその確率は０％では無い。 つまり、絶対に出ない、という訳では無い。 正規分布ではx軸が漸近線である、というのは、このこと。

---

「キーワード辞典」の目次へ