Ｒｙｎのページ（商業高校情報教育研究室）

ベルヌーイ試行

コイントスなど、何かを行った際に一定の確率で２つの結果のみ起きる試行のことを「ベルヌーイ試行」と言う。 ベルヌーイ試行では、一般に、２つの結果のうち片方を「成功」「１」とし、もう片方を「失敗」「０」とする。
コイントスは、表が出るか（成功）、裏が出るか（失敗）とすると、その確率はどちらも２分の１、 サイコロで、１の目が出るか（成功）、それ以外が出るか（失敗）とすると、 その確率は、成功は６分の１、失敗は６分の５となる。

二項分布

ベルヌーイ試行をｎ回繰り返す事によって、 Ｘ軸をｎ回の内で成功する回数ｋ、Ｙ軸をｋ回成功する確率として描かれる山型の分布を二項分布と言い、 ｎ回の内でｋ回成功する確率は、 繰り返す回数をｎ、その内で成功する回数をｋ、成功する確率をｐ（０≦ｐ≦１）とすると、

で求められる。

_ｎＣ_ｋ は、ｎ回の内でｋ回成功する組み合わせの数、 ｐ^ｋ は、ｋ回成功する確率、 （１－ｐ）^ｎ－ｋ は、残りのｎ－ｋ回を失敗する（＝１－ｐ）確率で、 この３つを掛け合わせたものとなる。

また、期待値（平均値) μは、試行回数ｎ×成功確率ｐ、 分散 σ²は、試行回数ｎ×成功確率ｐ×失敗する確率１ーｐ、 で求められることが判って居る。

二項分布は、

• 試行の結果は成功か失敗かどちらかであること。
• 各試行は独立である（前の試行が後の試行の確率に影響を与えない）こと。
• 成功確率と失敗確率は常に一定であること。

が条件となる。

Excelで二項分布のグラフを描く

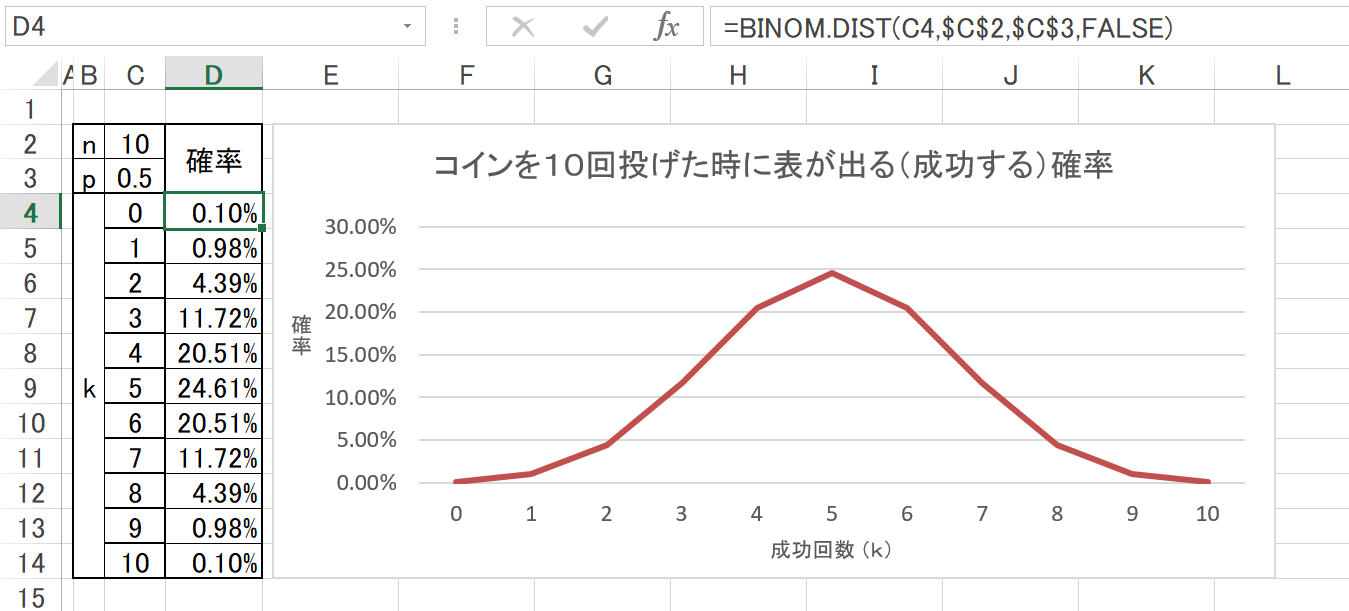
コインの例。
関数は、「 = BINOM.DIST ( ｋの値, ｎの値, ｐの値, FALSE )。
10回の内で5回成功する確率が最も高い。

10回の内で成功する平均回数 μ は、10 × 1 2 ＝ 5。
分散 σ² は、10 × 1 2 × ( 1 - 1 2 ) ＝ 2.5。

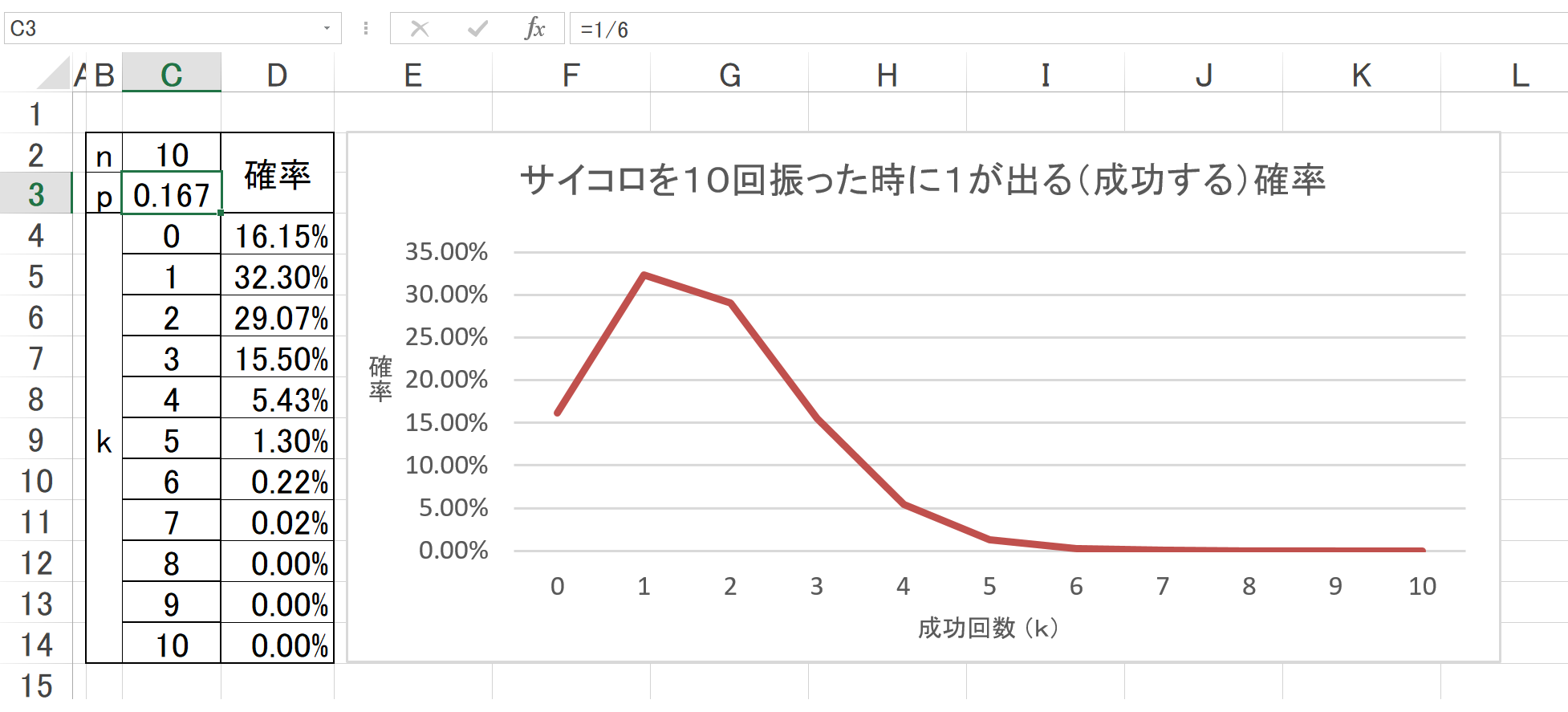
サイコロの例。
セルＣ３の数式は、「＝１／６」。
セル幅の都合上で見た目は０％表示のセルも、実際は０％では無い。


10回の内で成功する平均回数 μ は、10 × 1 6 = 1.666...。
分散 σ² は、10 × 1 6 × ( 1 - 1 6 ) ＝ 1.3888...。

成功確率ｐが小さい程、（なかなか成功しないので）左側に寄り、尖った山型になる。

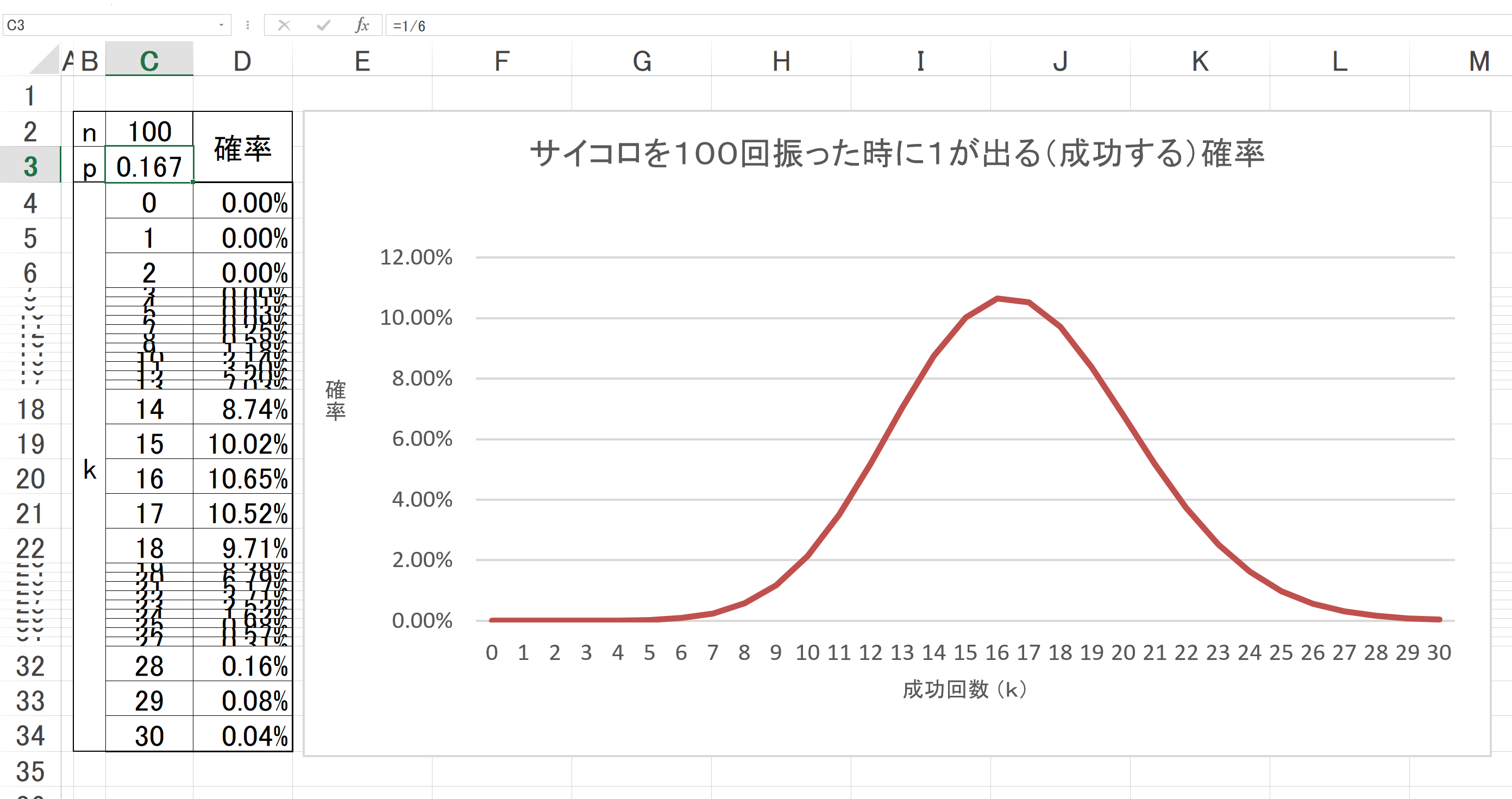
サイコロの例２。
サイコロを振る回数ｎを10回から100回に増やす。
グラフでは、横幅の都合によりＸ軸の成功する回数ｋを０から３０まで表示している。


100回の内で成功する平均回数 μ は、100 × 1 6 = 16.666...。
分散 σ² は、100 × 1 6 × ( 1 - 1 6 ) ＝ 13.888...。

此処から、試行回数ｎを 1000 に増やすと、グラフのＸ軸Ｙ軸の目盛が等しければ、 ｎ＝100と比較して更に低く滑らかな山型になり、 成功する回数ｋの平均 μは、166.666... になることが推測出来る。

つまり、試行回数ｎが大きくなると、小数部分が整数部分になることで最頻値、中央値が平均μに近づき、 また、成功回数ｋの範囲が増える分だけ、各々の回数で成功する確率は小さくなる。

実際にやってみて、 「余りにも成功し過ぎるんじゃない？」と言う場合は、コインやサイコロ、 或いは試行の仕方を疑う場合も有る、かも。 それは、別の項で。

---

「キーワード辞典」の目次へ