Ｒｙｎのページ（商業高校情報教育研究室）

公開鍵暗号方式

暗号化と復号とに別の鍵を使い、暗号化の為の鍵を公開できるようにした暗号方式。 暗号化する鍵が公開されている為、共通鍵暗号方式に見られる様な問題が起きず、 復号する鍵を本人だけが持つことで盗聴を防ぐ。 有名なものにＲＳＡが有るが、ＲＳＡだけが公開鍵暗号方式では無いので、 混同してはいけない。

ＲＳＡ

有名な公開鍵暗号方式のアルゴリズムの一つ。 片方の鍵で暗号化するともう片方の鍵でないと復号出来ない関係を持つ一対の鍵を使用する。 片方を誰でも使える公開鍵、もう片方を自分だけの秘密鍵にし、 送信時の暗号化に受信者の公開鍵、受信時の復号に受信者の秘密鍵、を使用することで、 誰でも暗号化が出来るがそれを復号出来るのは受信者のみとなる。
ＲＳＡは、開発した３人の技術者の頭文字。

「２つの素数ｐ、ｑの積Ｎを法（Ｎ－１までしか数が存在せず１を加えると０に戻る）とする、 計数機の様な世界では、 或る数を、 ｎ×（ｐ－１とｑ－１の最小公倍数）＋１）乗した値は、元の数と等しくなる（ｎは任意の整数）」 ことを利用している。
具体的には、

1. ２つの素数ｐとｑを決める。
2. ｐとｑを掛けて法Ｎを求める。
3. (p-1)と(q-1)の最小公倍数Ｌを求める。
   Ｌは、元の数に戻る、べき乗数の周期。
   Ｌ＋１は、１乗を除き、最初に元の数に戻る時のべき乗数。
4. ｅ×ｄを(p-1)×(q-1)で割った余りが１となり、 ３以上でＬより小さく、Ｌとの最大公約数が１（＝互いに素）である、 整数ｅと整数ｄを決める。
5. Ｎとｅが公開鍵、Ｎとｄが秘密鍵になる。
6. 暗号化は、公開鍵を使って、暗号文＝平文^ｅ ｍｏｄ Ｎ
   復号は、秘密鍵を使って、平文＝暗号文^ｄ ｍｏｄ Ｎ
   

RynもEXCELでやってみた。
２つの素数ｐ＝３、ｑ＝１１とすると、法Ｎは３３。
（ｐ－１）の２と（ｑ－１）の１０との最小公倍数Ｌは１０。
（ｅ×ｄ）ｍｏｄ（（ｐ－１）×（ｑ－１））＝１で、３以上Ｌ未満、Ｌと互いに素である、ｅとｄを求める。
ｅ＝７、ｄ＝３、とすると、
（７×３）ｍｏｄ（２×１０）＝１となる。

例１（図の赤丸）
平文３を暗号化する場合は、公開鍵（Ｎ＝３３，ｅ＝７）を使って、３^７ ｍｏｄ ３３＝９
暗号文９を復号する場合は、秘密鍵（Ｎ＝３３，ｄ＝３）を使って、９^３ ｍｏｄ ３３＝３

例２（図の緑丸）
平文８を暗号化する場合は、公開鍵を使って、８^７ ｍｏｄ ３３＝２
暗号文２を復号する場合は、秘密鍵を使って、２^３ ｍｏｄ ３３＝８




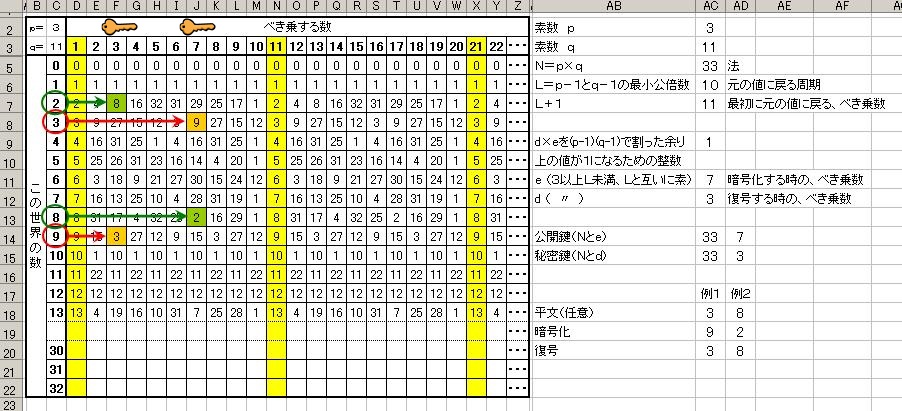
小さい数では余り面白くないが、 非常に大きな数においては、素数×素数の計算は簡単だが、 因数分解した２つの数値が素数かどうかを調べるのは無茶苦茶時間がかかる事から、 経験則としてセキュリティが高いとされている。 しかし、アルゴリズムが複雑で処理に時間がかかるので、 通常は平文全体をＲＳＡ方式で暗号化する事はせず、 送信者は、平文を、その時限りで作成した共通鍵暗号方式の秘密鍵（セション鍵）で暗号化し、 その秘密鍵をＲＳＡ方式の受信者の公開鍵で暗号化して、 暗号文と暗号化されたセション鍵の２つを送信する事が多い。 受信者は、ＲＳＡ方式の自分だけの秘密鍵でセション鍵を復号した後、 そのセション鍵を使って暗号文を復号する。

物凄く乱暴な一例
実際はもっと複雑な処理をしています。勿論。

• 平文
  「６時に駅」→「ロクジニエキ」
• セション鍵
  例として、五十音順にずらす文字数を鍵にする。暗号化は前へ、復号は後へずらす。今回は３とする。
• 公開鍵と秘密鍵
  上記のもの。

送信者の暗号化手順

1. 平文をセション鍵３で暗号化する。
   「ロクジニエキ」→「リオゲテアエ」
2. セション鍵３を受信者の公開鍵（３３と７）で暗号化する
   ３^７ ｍｏｄ ３３＝９
3. 暗号文「リオゲテアエ」と暗号化されたセション鍵９を相手に送付する

受信者の復号手順

1. セション鍵９を受信者の秘密鍵（３３と３）で復号する
   ９^３ ｍｏｄ ３３＝３
2. 復号されたセション鍵３を使って、暗号文を復号する。
   「リオゲテアエ」→「ロクジニエキ」

---

「キーワード辞典」の目次へ