Ｒｙｎのページ（商業高校情報教育研究室）

加算・減算の前提

コンピュータはハードウェアとして論理回路を組み合わせれば様々な機能の回路を作る事が出来、 一方、命令も、マイクロコードといったソフトウェアによって、同様に様々な機能を実現する事が出来るが、 その機能をハードウェアの回路で実現するか、 基本的な回路とマイクロコードといったソフトウェアで実現するか、という問題は有る。 以下は、四則演算のハードウェアとしては加算器のみが有る、という前提でマイクロコード的な説明をする。

コンピュータは何故補数を使うのか？

コンピュータはハードウェアとしては加算をする回路（加算器）しか持たず、 また、或る桁のビットの加算の結果を上位の桁に送る事は可能（全加算器）ですが、上位の桁から借りて来て、というのは苦手です。 しかし、ビットを反転させるＮＯＴ演算は得意です。 よって、減算をしたい場合は、ビットの反転と加算だけで出来る補数を利用し、 ａ－ｂではなく、ａ＋（－ｂ）という形で行います。 そのために、以下の様な考え方をします。

整数で、桁溢れを無視する前提で、 ビット列10...0 を最小値、其処から１ずつ加えて行き、0...0 をゼロ、01...1 を最大値 と定義した場合、 減算は符号を反転した値を加算する事で出来、その際、符号を反転したビット列は元の値の２の補数で求められる。 但し最大値の２の補数は最小値にならず、最小値は最大値の１の補数になる。

整数のみ、桁溢れをしない世界

左の写真は一般的に日常で使われる十進法４桁の計数器です。
上のカウントアップボタンを押すと値が１ずつ加算され、
9999の次は0000に戻ります。 また、横のリセットボタンを押すとスタートの値、0000に戻ります。

カウントアップ→

十進表記 … 0000 0001 0002 0003 … 0008 0009 0010 0011 0012 … 9997 9998 9999 0000 …

十進の値 …  ０   １   ２   ３  …  ８   ９  １０ １１ １２  … 

仮に、二進法４桁だけで整数のみが表現出来る世界があるとします。 しかも、この世界には加算しかありません。
左の写真は世にも珍しい二進法の計数器（ウソ）で、上のカウントアップボタンを押すと値が１ずつ加算され、
1111の次は0000に戻ります。 また、横のリセットボタンを押すとスタートの値に戻ります。
スタートの値は、0000とは限りませんが、十進法のゼロは、0000です。

カウントアップ→

二進表記 … 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 0000 …

十進の値 …  ０   ？   ？   ？   ？   ？   ？   ？   ？   ？   ？   ？   ？   ？   ？   ？   ０  …

正の数値だけの世界

二進表記の0000をカウントアップのスタートの値とし、その値を０と定義すると、次の様になります。

カウントアップ→

二進表記 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

十進の値  ０   １   ２   ３   ４   ５   ６   ７   ８   ９  １０ １１ １２ １３ １４ １５

表現出来るのは十進の値でいう０から１５までで、 加算した結果が１５を超えると、表現出来なくなります。

正と負が有る世界

以下、面倒臭いので、二進表記は、適宜、下線を引きます。

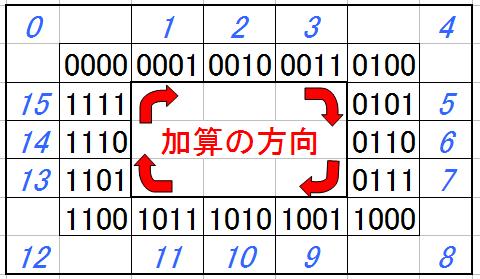この世界は桁数が４桁しか無いため、例えば、 1111（十進表記で１５）に0001（十進表記で１）を加算すると、 解は10000ではなく、あふれた桁が無視されて0000（十進表記で０）に戻る、 リング状の双六の様な状態になっています。

したがって、1111を十進法の１５と定義した場合、 0001は十進法の正の数１をあらわすと同時に、 1111に0001を加算した結果が０になるのだから、１５＋（－１５）＝０で、 十進表記の負の数である－１５と同じ意味でもあると言うことが出来ます。

二進表記 1111 ＋ 0001 ＝ 0000

十進の値 １５ ＋  ？  ＝  ０　　→　？＝－１５

あるいは、0001を十進法の１と定義した場合は、 1111は十進法の正の数１５をあらわすと同時に、 １＋（－１）＝０で、十進法の負の数である－１と同じ意味でもあると言うことも出来ます。

二進表記 0001 ＋ 1111 ＝ 0000

十進の値  １  ＋  ？  ＝  ０　　→　？＝－１

同様に、それぞれは、

二進表記 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

十進の値  ０   １   ２   ３   ４   ５   ６   ７   ８   ９  １０ １１ １２ １３ １４ １５　正の数値だけ

十進の値  ０  -15  -14  -13  -12  -11  -10 －９ －８ －７  －６ －５ －４ －３ －２ －１　０と負の数値だけ

の意味を持たせる事が出来ます。

しかし、１つの二進表記に対して２つの値を持たせるのでは大混乱するし、 正の数だけ、或いは０と負の数だけ、の世界では不便な場合も有るので、 十進の値で正の数値だけの世界との互換性を含めて、 左端のビットが０ならば正の数、１ならば負の数という事に決めると、

二進表記 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

十進の値  ０   １   ２   ３   ４   ５   ６   ７  －８ －７ －６ －５ －４ －３ －２ －１

となり、これを十進の値の昇順に並び替えると、

カウントアップ→

二進表記 1000 1001 1010 1011 1100 1101 1110 1111 0000 0001 0010 0011 0100 0101 0110 0111

十進の値 －８ －７ －６ －５ －４ －３ －２ －１  ０   １   ２   ３ 　４   ５   ６   ７

となります。 冒頭の計数器で言えば、 二進表記の1000をカウントアップのスタートの値とし、その値を十進の－８と定義した状態です。 つまり、この考え方を利用すれば、十進法で－８から７までの値を表現出来る事になります。 これが、冒頭で書いた内容です。

例えば、正の数ー正の数では、
十進表記の、５－１ ＝ ５＋（－１）＝ ４、二進表記では、0101ー0001＝0101＋1111＝10100 → 0100
十進表記の、２－３ ＝ ２＋（－３）＝ －１、二進表記では、0010ー0011＝0010＋1101＝1111
となります。

同様に、正の数ー負の数では、
十進表記の、５－（ー１） ＝ ５＋１＝ ６、二進表記では、0101ー1111＝0101＋0001＝0111
十進表記の、２－（ー３） ＝ ２＋３＝ ５、二進表記では、0010ー1101＝0010＋0011＝0101

負の数ー正の数では、
十進表記の、ー５－１ ＝ ー５＋（－１）＝ ー６、二進表記では、1011ー0001＝1011＋1111＝11010 → 1010
十進表記の、ー２－３ ＝ ー２＋（－３）＝ －５、二進表記では、1110ー0011＝1110＋1101＝11011 → 1011

負の数ー負の数では、
十進表記の、ー５－（ー１） ＝ ー５＋１＝ ー４、二進表記では、1011ー1111＝1011＋0001＝1100
十進表記の、ー２－（ー３） ＝ ー２＋３＝ １、二進表記では、1110ー1101＝1110＋0011＝10001 → 0001
となります。

ただし、「正の整数＋正の整数」の解が負の数になったり、 「負の整数＋負の整数」の解が正の数になったりする場合は、 その解が本来はこの世界に存在していない値のために表現出来ない状態なので、注意が必要です。

---

「キーワード辞典」の目次へ